17. Statistical item list
It explains on how to obtain the respective statistical value and
its outline on the data
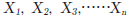 of n item.
of n item.
| Statistical item | Calculation formula, explanation |
|---|---|
|
Arithmetic MeanArithmetic average |
Arithmetic Mean is also called Arithmetic average, and given by the following formula. It shows the Arithmetic mean when generally said average. It is necessary to note when included extreme outlier, and irregular distribution. |
|
Geometrical average (geometrical mean) |
Geometrical average is also called average geometrical mean, and given by the following formula. It is used when calculating the average of “ratio” such as growth rate, deterioration rate. Note that it can not use to calculate for negative value. |
|
Harmonic Mean |
The harmonic mean is given by the following formula. Note that it can not use to calculate data including 0. |
|
2 root mean square |
2 Root mean square is given by the following formula. |
|
Weighted Mean |
Weighted mean is given by the following formula when
the weight for each data
|
|
MedianMedian |
The median is really the middle. Order the numbers, smallest to largest and pick the middle one; that’s the median. |
|
ModeMode |
The most frequently occurring number in a list is called the mode. |
|
RangeRange |
Range is the value subtracted the minimum value (Xmin)
from maximum value (Xmax) of data and is given by the
following formula. |
|
Deviation |
The value subtracted the Arithmetic Mean value from each data is given by the following formula. It is an index that shows how much the individual data is away from the Arithmetic Mean value. |
|
Sum of squared deviation |
The value totaled with 2 power value of deflection is given by the following formula. It is an index that shows the variation of the entire data. There is polarity in the individual deviation, so totals the 2 power because it becomes zero if simply totaled. |
|
Sample Variance |
The sample variance is shown by the following formula and is provided by the value in which the sum of squared deviation is divided by number of samples n. The variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean (expected value). It is one of the the second indices that show the variance condition of the entire data. Sample of the sample variance shows the variance for the sample (or test piece) when sampling is performed for a certain population. Therefore, (Sample =population) does not require (sample) when dealing with data of the entire population. Unbiased variance will be prioritized that will be described later for the estimation value of population variance Population Variance. |
|
Sample Standard Deviation |
The sample standard deviation is given by the value in which the square root of the sample variance is taken by the following formula It becomes an index to show the variance condition of the entire data. “Sample” shows sampling similar to sample variance. Unbiased Standard Deviation will be prioritized that will be described later for the estimation value of Population standard deviation Population Standard Deviation. |
|
Unbiased variance |
The unbiased variance is given by the following
formula by the value divided by
Here
|
|
Unbiased Standard Deviation |
Unbiased Standard Deviation is a value that take square root of unbiased variance and is given by the following formula. Estimate value of population standard deviation is more prioritized than sample standard deviation. |
|
Deviation value |
The deviation value of a certain data X is given by the following formula. The deviation value is a dimensionless index that shows how much a certain data is located within the population. 50 is considered when the data is equal to the universe mean, and the variation from there considers the variation of the population standard deviation equivalent to 10. |
|
Normal Distribution |
Normal distribution is in hanging bell type, and is the mostly used distribution as the distribution of the population for the phenomenon led by a coincidental nature, and it given by the following formula. μ shows the average, σ shows standard deviation. Normal distribution is expressed by N(μ, σ). The calculation value of standard normal distribution N(0, 1) can be read in the attached normal distribution table. |
|
Additivity of variance |
There is relation with
between the relation of variable
Therefore, the following formula is also established. This shows the possibility to meet excessive margin in the worst design method by simply adding the variations when doing the combined design of the independent variation. For example, standard deviation is not the 2 times of standard deviation of simplex, but it is the square roots of 2 (1.414 times) when 2 items having the same variations are combined. |
