17. 統計項目一覧
n個のデータ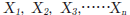 に対し、それぞれの統計値の求め方と、その概要を説明します。
に対し、それぞれの統計値の求め方と、その概要を説明します。
| 統計項目 | 算出式及び、説明 |
|---|---|
|
相加平均(算術平均) |
相加平均は算術平均とも呼ばれ、以下の式で与えられます。 通常、単に平均と言った場合、この相加平均を示します。極端な外れ値を含んでいたり、分布が歪んでいる場合に代表性が弱くなるので注意が必要です。 |
|
相乗平均(幾何平均) |
相乗平均は幾何平均とも呼ばれ、以下の式で与えられます。 成長率や悪化率などの、「率」の平均を計算する際に用いられます。マイナスの値は扱えないので注意が必要です。 |
|
調和平均 |
調和平均は以下の式で与えられます。 0を含んだデータには使えないので注意が必要です。 |
|
2乗平均平方根 |
2乗平均平方根は以下の式で与えられます。 |
|
加重平均 |
各データ |
|
中央値(Median) |
中央値は、各データを小さい順に並べたときの中央に位置する値です。データの数が偶数の場合は、中央に近い2つのデータの相加平均をとります。外れ値を含む場合や、歪んだ分布に強い代表値です。 |
|
最頻値( Mode) |
最頻値は、各データの度数分布を考慮した場合、最も度数が高い(最も多く現れる)データの値です。 |
|
範囲(Range) |
範囲は、データの最大の値(Xmax)から最小の値(Xmin)を引いた値で、以下の式で与えられます。 |
|
偏差 |
各データから相加平均値を引いた値で、以下の式で与えられます。 個々のデータが相加平均値から、どれだけ離れているかを示す指標です。 |
|
偏差平方和 |
偏差の2乗値を合計した値で、以下の式で与えられます。 データ全体のばらつきを示す指標です。個々の偏差には極性があり単純に合計してしまうとゼロになってしまうため、2乗したものを合計します。 |
|
標本分散 |
標本分散は偏差平方和を標本数 n で割った値で、以下の式で与えられます。 データ全体のばらつき具合を示す2次の指標の1つとなります。標本分散の「標本」とは、ある母集団に対しサンプリングを行った場合の標本(または試料)に対しての分散であることを示すものです。従って、母集団全てのデータを扱う場合(標本=母集団)は「標本」は必要ありません。標本分散に対して、母集団分散(Population Variance)の推定値としては後述する不偏分散の方が優れています。 |
|
標本標準偏差 |
標本標準偏差は、標本分散の平方根をとった値で、以下の式で与えられます。 データ全体のばらつき具合を示す1つの指標となります。標本分散と同様に、「標本」はサンプリングされたことを示します。母集団標準偏差(Population Standard Deviation)の推定値としては後述する不偏標準偏差の方が優れています。 |
|
不偏分散 |
不偏分散は、偏差平方和を
ここで |
|
不偏標準偏差 |
不偏標準偏差とは、不偏分散の平方根をとった値で、以下の式で与えられます。 母集団標準偏差の推定値としては、標本標準偏差よりも優れています。 |
|
偏差値 |
あるデータXの偏差値は以下の式で与えられます。 偏差値とは、あるデータが母集団の中でどれくらいに位置しているかを示す無次元の指標です。データが母集団平均に等しい場合を50とし、そこからのばらつきは母集団標準偏差相当のばらつきを10としています。 |
|
正規分布 |
正規分布は釣鐘型をしており、偶然性に支配された現象の母集団の分布として最も良く使われる分布であり、以下の式で与えられます。 ( μは平均、σは標準偏差を示す) 正規分布は N(μ, σ)で表現されます。 標準正規分布 N(0, 1)の計算値は、添付されている正規分布表で読み取ることができます。 |
|
分散の加法性 |
変数
の関係があり、全ての
よって、以下の式も成立します。 これは、独立のばらつきを持つものを組み合わせ設計する場合に、単純にばらつきを足し合わせる最悪状態設計法では過剰にマージンを見てしまう可能性があることを示しています。例えば、同じばらつきを持つ2個の部品を組み合わせた場合の標準偏差は、単体の標準偏差の2倍ではなく、2の平方根(1.414倍)となることから分かります。 |
