17. 통계 항목 일람
n개의 데이터
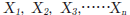 에 대하여 각각의 통계치 구하는 법과 그 개요를 설명합니다.
에 대하여 각각의 통계치 구하는 법과 그 개요를 설명합니다.
| 통계 항목 | 산출식 그리고 설명 |
|---|---|
|
상가 평균 (산술 평균) |
상가 평균은 산술 평균이라고도 하고 다음과 같은 식으로 표현됩니다. 일반적으로 단순히 평균이라고 하면 상가 평균을 나타냅니다. 극단적인 이상치를 포함하거나 분포가 왜곡되어 있으면 대표성이 약해지기 때문에 주의가 필요합니다. |
|
상승 평균 (기하 평균) |
상승 평균은 기하 평균이라고도 하고 다음과 같은 식으로 표현됩니다. 성장률과 악화율 등, ‘율’의 평균을 계산할 때에 사용됩니다. 마이너스 값은 다룰 수 없으므로 주의가 필요합니다. |
|
조화 평균 |
조화 평균은 다음의 식으로 표현됩니다. 0을 포함한 데이터에는 사용할 수 없으므로 주의가 필요합니다. |
|
제곱 평균 제곱근 |
제곱 평균 제곱근은 다음과 같은 식으로 표현됩니다. |
|
가중 평균 |
각 데이터
|
|
중앙값(Median) |
중앙값은 각 데이터를 작은 순으로 정렬했을 때 중앙에 있는 값입니다. 데이터의 수가 짝수이면 중앙에 가까운 2개의 데이터의 상가 평균을 사용합니다. 이상치를 포함하는 경우와 왜곡된 분포에 강인한 대표값입니다. |
|
최빈값( Mode) |
최빈값은 각 데이터의 도수 분포를 고려했을 경우 가장 도수가 높은(가장 많이 나타나는) 데이터의 값입니다. |
|
범위(Range) |
범위는 데이터의 최댓값(Xmax)에서 최솟값(Xmin)을 뺀
값으로 다음과 같은 식으로 표현됩니다. |
|
편차 |
각 데이터에서 상가 평균값을 뺀 값으로 다음과 같은 식으로 표현됩니다. 각각의 데이터가 상가 평균값으로부터 어느 정도 떨어져 있는지를 나타내는 지표입니다. |
|
편차 제곱합 |
편차의 제곱을 합산한 값으로 다음과 같은 식으로 표현됩니다. 데이터 전체의 산포도를 나타내는 지표입니다. 각각의 편차에는 양수, 음수가 있으므로 단순히 합산하면 0이 되어버리기 때문에 제곱한 값을 합산합니다. |
|
표본 분산 |
표본 분산은 편차 제곱합을 표본 수 n으로 나눈 값으로 다음과 같은 식으로 표현됩니다. 데이터 전체의 산포도 상태를 나타내는 2차 지표 중의 하나입니다. 표본 분산의 ‘표본’이란 어떠한 모집단에 대하여 샘플링을 했을 경우의 표본(또는 시료)에 대한 분산이라는 것을 나타내는 용어입니다. 따라서 모집단 전체의 데이터를 다루는 경우(표본=모집단)에는 ‘표본’은 필요가 없습니다. 표본 분산에 대한 모집단 분산(Population Variance)의 추정치로서는 후술하는 불편 분산이 더 우수합니다. |
|
표본 표준 편차 |
표본 표준 편차는 표본 분산의 제곱근을 구한 값으로 다음과 같은 식으로 표현됩니다. 데이터 전체의 산포도 상태를 나타내는 하나의 지표입니다. 표본 분산과 같이 ‘표본’은 샘플링되었다는 것을 나타냅니다. 모집단 표준편차(Population Standard Deviation)의 추정치로서는 후술하는 불편 표준 편차가 더 우수합니다. |
|
불편 분산 |
불편 분산은 편차 제곱합을
여기서
|
|
불편 표준 편차 |
불편 표준 편차란 불편 분산의 제곱근을 구한 값으로 다음과 같은 식으로 표현됩니다. 모집단 표준 편차의 추정치로서는 표본 표준 편차보다 더 우수합니다. |
|
표준 점수 |
어떠한 데이터의 표준 점수는 다음과 같은 식으로 표현됩니다. 표준 점수란 어떤 데이터가 모집단 중에서 어느 정도에 있는지를 나타내는 무차원의 지표입니다. 데이터가 모집단 평균과 같은 경우를 50으로 하고 그곳으로부터의 산포도는 모집단 표준 편차에 상당하는 산포도를 10으로 하고 있습니다. |
|
정규 분포 |
정규 분포는 종과 같은 형태를 하고 있고 우연성에 지배되는 현상의 모집단 분포로서 가장 많이 사용되는 분포로서 다음의 식으로 표현됩니다. ( μ는 평균, σ는 표준 편차를 나타냄) 정규 분포는 N(μ, σ)으로 표현됩니다. 표준 정규 분포 N(0, 1)의 계산값는 첨부된 정규 분포표로 확인할 수 있습니다. |
|
분산의 가법성 |
변수
의 관계가 있고 모든
에 의해 다음의 식도 성립합니다. 이것은 독립한 산포도를 가지는 것을 조합하여 설계하면 단순히 산포도를 더하는 최악의 상태 설계법으로는 과도하게 그 차이를 보게 될 가능성이 있음을 나타냅니다. 예를 들면 같은 산포도를 가지는 2개의 부품을 조합한 경우의 표준 편차는 단품의 표준 편차의 2배가 아니고 2의 제곱근(1.414배)이 되는 것으로부터 알 수 있습니다. |
