18. Laplace transform
If Laplace transform is used, the difficult calculation of
derivation and integration required in the design of the control
circuit can be replaced with the simple multiplication, division
calculation of algebra operation. Laplace transform is defined as
follows.
Fs defined by
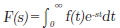 on the time function ft defined by t≧0 is called the Laplace
transform of f(t). The list of Laplace transform of the
fundamental function is shown below.
on the time function ft defined by t≧0 is called the Laplace
transform of f(t). The list of Laplace transform of the
fundamental function is shown below.
| Function name | Time function f(t) | Laplace transform F(s) |
|---|---|---|
|
Unit impulse function |
δ(t) |
1 |
|
Unit step function |
1 |
|
|
Unit ramp function |
t |
|
|
|
|
|
|
Exponential function |
|
|
Sine function |
sin ωt |
|
Cosine function |
cos ωt |
|
|
Hyperbolic sineSineFunction |
sinh ωt |
|
|
Hyperbolic cosineCosineFunction |
cosh ωt |
|
sinc Function |
|
|
|
Other functions |
|
|
|
|
|
|
|
|
|
|
t sin ωt |
|
|
t cos ωt |
|
