18. 라플라스 변환
라플라스 변환을 이용하면 제어 회로의 설계에 필요한 미분, 적분과
같은 어려운 연산을 간단한 곱셈, 나눗셈과 같은 대수 연산으로
치환하는 것이 가능합니다. 라플라스 변환은 다음과 같이 정의됩니다.
t≧0의 범위 안에서 정의된 시간 함수 f(t)에 대하여
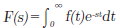 로 정의되는 F(s)를 f(t)의 라플라스 변환이라고 합니다. 오른쪽 표는
기본 함수의 라플라스 변환을 나타냅니다.
로 정의되는 F(s)를 f(t)의 라플라스 변환이라고 합니다. 오른쪽 표는
기본 함수의 라플라스 변환을 나타냅니다.
| 함수명 | 시간 함수 f(t) | 라플라스 변환 F(s) |
|---|---|---|
|
단위 임펄스 함수 |
δ(t) |
1 |
|
단위 스텝 함수 |
1 |
|
|
단위 램프 함수 |
t |
|
|
|
|
|
|
지수 함수 |
|
|
|
사인 함수 |
sin ωt |
|
|
코사인 함수 |
cos ωt |
|
|
쌍곡선 사인 함수 |
sinh ωt |
|
|
쌍곡선 코사인 함수 |
cosh ωt |
|
|
sinc 함수 |
|
|
| 그 이외의 함수 |
|
|
|
|
|
|
|
|
|
|
|
t sin ωt |
|
|
|
t cos ωt |
|
