18. ラプラス変換
ラプラス変換を用いれば、制御回路の設計で必要になる微分・積分の難しい演算が、簡単な掛け算・割り算の代数演算に置き換えることができます。ラプラス変換は以下のように定義されます。
t≧0で定義された時間関数f（t）に対して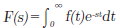
で定義されるF（s）をf（t）のラプラス変換と言います。右に基本関数のラプラス変換を示します。
| 関数名 | 時間関数 f(t) | ラプラス変換 F(s) |
|---|---|---|
|
単位インパルス関数 |
δ(t) |
1 |
単位ステップ関数 |
1 |
|
|
単位ランプ関数 |
t |
|
|
|
|
指数関数 |
|
|
サイン関数 |
sin ωt |
|
コサイン関数 |
cos ωt |
|
|
双曲線正弦（サイン）関数 |
sinh ωt |
|
|
双曲線余弦（コサイン）関数 |
cosh ωt |
|
sinc関数 |
|
|
|
その他の関数 |
|
|
|
|
|
|
|
|
t sin ωt |
|
|
t cos ωt |
|